Posted 01 July 2017
I went down a bit of a rabbit-hole between my last post on this subject and today. I was attempting to run down the problems with my IR demodulation code when I discovered that the basic rate at which the demodulator captured samples was off by a factor of 5 or so – yikes!! Instead of 20 samples per cycle, I was seeing more like 100, as shown below.
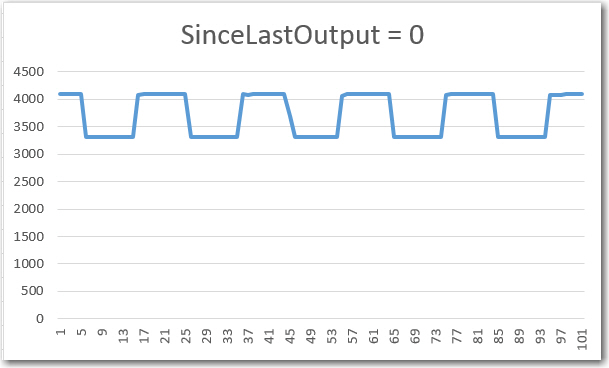
Raw data capture using ‘sinceLastOutput = 0’ in the first demodulation step
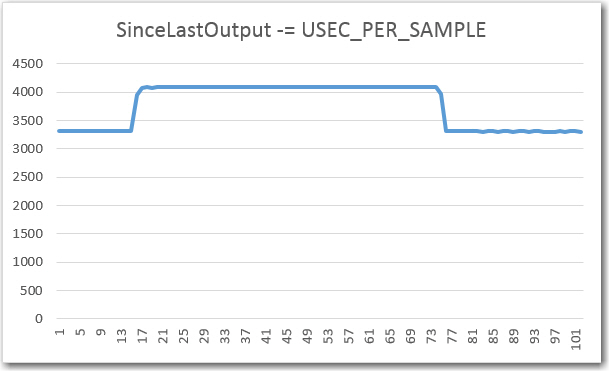
Raw data capture using ‘sinceLastOutput -= USEC_PER_SAMPLE’ in the first demodulation step
As you might expect, this development threw me for a bit of a loop – as the change from ‘sinceLastOutput = 0’ to ‘sinceLastOutput -= USEC_PER_SAMPLE’ was instrumental (or at least so I thought) to getting the transmit and receive frequencies matched more accurately. So, now I had to go chase down yet another tangential problem – what I refer to as ‘going down a rabbit hole’. The only saving grace in all this is that, as a twice-retired engineer, I have no deadlines!
To resolve this problem, I wound up creating an entirely new test program to isolate the issue, with just the following lines in the loop() function:
With the ‘sinceLastOutput -= USEC_PER_SAMPLE’ line active, I got about 100 samples/cycle. With this line commented out and the ‘sinceLastOutput = 0’ line active, I got the normal 20 samples/cycle, with nothing else being changed.
Once I was sure the test program was consistently producing the anomalous results I had noticed in the complete program, I posted this issue to the PJRC Forum, so I could get some help from the experts. I knew it was something I was doing wrong – I just didn’t know what!
Within a few hours I had received several responses, and the one that hit the bullseye was the one correctly identifying a subtlety with the the ‘-=’ elapsedMicros() usage format. When this format is used, the accompanying ‘elapsedMicros’ variable must be initialized in the setup() code; otherwise it will be some arbitrary (and possibly quite large) value when the loop() function is first entered. This will cause the ‘if’ statement to trigger repeatedly until the ‘-=’ line eventually reduces the variable to a value below USEC_PER_SAMPLE, at which point it will start behaving as expected. This odd behavior never happens with the ‘=0’ usage, as the variable is initialized on the first pass through the ‘if’ statement. Sure enough, when I added a line at the bottom of my setup() function to set the ‘sinceLastOutput’ variable to zero, my little test program immediately stopped mis-behaving.
Well, this little side-journey only cost me a couple of days, and a few more white hairs (oh, wait – my hair is already completely white – no problem!) Back to my regularly scheduled program…
Frequency Matching:
My friend and mentor John Jenkins, who has been looking over my shoulder (and occasionally whacking me on the head) during this project, was unsure that my frequency matching setup was actually 100% complete, as the video I took the last time didn’t run long enough to convince him (and there were some un-explained triggering glitches as well). So, I thought I would re-do this part to make him happy. To do this I modified my little test program from the above ‘rabbit-hole’ elapsedMicros issue to output a square wave from the demodulator board that could be compared to the transmitter square wave.
As shown in the above video, the transmit and demodulator frequencies are quite well matched, showing essentially zero relative drift even over the 30-40 second time of the video. Mission accomplished! ;-).
Sample Acquisition Step:
I modified my demodulator program to properly initialize the ‘elapsedMicros’ variable being used for sample timing, and verified proper operation by commenting out everything but the sample acquisition step. I captured several hundred samples, and plotted the first hundred in Excel as follows:
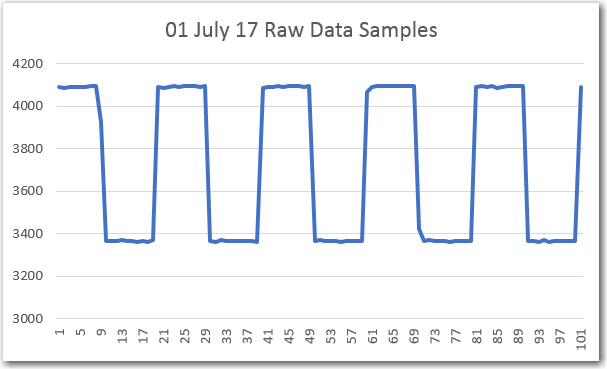
100 samples using proper ‘elapsedMicros’ variable initialization
Sample Sum Step:
Next, each group of five samples (1/4 cycle) is summed, and the ‘In-phase’ and ‘Quadrature’ components are generated using the appropriate sign sequences. As shown in the following, this appears to be happening correctly:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 |
Opening port Port open SI Samp GSumI GSumQ 0 4089 1 4091 2 4092 3 4095 4 3392 19759 -19759 5 3390 6 3395 7 3390 8 3389 9 3390 16954 16954 10 3388 11 3388 12 3390 13 3387 14 4081 -17634 17634 15 4090 16 4093 17 4092 18 4093 19 4093 -20461 -20461 20 4089 21 4092 22 4095 23 4095 24 3400 19771 -19771 25 3387 26 3391 27 3386 28 3389 29 3389 16942 16942 30 3388 31 3389 32 3386 33 3383 34 3756 -17302 17302 35 4090 36 4090 37 4092 38 4091 39 4091 -20454 -20454 40 4095 41 4095 42 4094 43 4093 44 4093 20470 -20470 45 3389 46 3389 47 3386 48 3391 49 3391 16946 16946 50 3391 51 3389 52 3392 53 3390 54 3388 -16950 16950 55 4089 56 4092 57 4095 58 4093 59 4094 -20463 -20463 60 4093 61 4095 62 4093 63 4095 64 4095 20471 -20471 65 3391 66 3392 67 3386 68 3390 69 3395 16954 16954 70 3388 71 3387 72 3387 73 3395 74 3391 -16948 16948 75 4085 76 4095 77 4092 78 4095 79 4093 -20460 -20460 80 4091 81 4095 82 4088 83 4090 84 4095 20459 -20459 85 3391 86 3386 87 3390 88 3387 89 3386 16940 16940 90 3389 91 3390 92 3389 93 3387 94 3387 -16942 16942 95 4047 96 4081 97 4082 98 4090 99 4095 -20395 -20395 100 4095 101 4095 102 4095 103 4095 104 4095 20475 -20475 105 4094 106 3390 107 3391 108 3390 109 3387 17652 17652 110 3386 111 3387 112 3386 113 3389 114 3391 -16939 16939 115 3394 116 4088 117 4090 118 4090 119 4093 -19755 -19755 120 4093 121 4090 122 4094 123 4095 124 4091 20463 -20463 125 4095 126 3388 127 3390 128 3389 129 3390 17652 17652 130 3391 131 3387 132 3387 133 3386 134 3390 -16941 16941 135 3390 136 4094 137 4094 138 4091 139 4094 -19763 -19763 140 4093 141 4095 142 4093 143 4093 144 4095 20469 -20469 145 4094 146 3385 147 3389 148 3391 149 3387 17646 17646 150 3387 151 3389 152 3390 153 3390 154 3386 -16942 16942 155 3382 156 4072 157 4089 158 4093 159 4092 -19728 -19728 160 4095 161 4094 162 4095 163 4095 164 4093 20472 -20472 165 4095 166 3450 167 3395 168 3394 169 3390 17724 17724 170 3392 171 3389 172 3390 173 3384 174 3389 -16944 16944 175 3389 176 3389 177 4093 178 4093 179 4090 -19054 -19054 180 4095 181 4095 182 4095 183 4094 184 4095 20474 -20474 185 4091 186 4095 187 3390 188 3387 189 3389 18352 18352 190 3390 191 3390 192 3389 193 3389 194 3388 -16946 16946 195 3388 196 3387 197 4091 198 4088 199 4091 -19045 -19045 200 4093 201 4094 202 4095 203 4095 204 4095 20472 -20472 205 4093 206 4093 207 3393 208 3386 209 3389 18354 18354 210 3388 211 3386 212 3389 213 3391 214 3389 -16943 16943 215 3388 216 3391 217 4080 218 4091 219 4095 -19045 -19045 220 4095 221 4095 222 4091 223 4095 224 4095 20471 -20471 225 4094 226 4089 227 3395 228 3390 229 3385 18353 18353 230 3386 231 3396 232 3387 233 3389 234 3391 -16949 16949 235 3387 236 3388 237 3858 238 4094 239 4091 -18818 -18818 240 4091 241 4095 242 4095 243 4095 244 4095 20471 -20471 245 4094 246 4089 247 4094 248 3401 249 3386 19064 19064 250 3388 251 3389 252 3393 253 3386 254 3390 -16946 16946 255 3390 256 3390 257 3392 258 4087 259 4090 -18349 -18349 260 4092 261 4094 262 4093 263 4095 264 4091 20465 -20465 265 4090 266 4095 267 4090 268 3394 269 3389 19058 19058 270 3391 271 3388 272 3390 273 3387 274 3385 -16941 16941 275 3386 276 3387 277 3389 278 4084 279 4095 -18341 -18341 280 4091 281 4093 282 4094 283 4093 284 4095 20466 -20466 285 4088 286 4093 287 4091 288 3388 289 3388 19048 19048 290 3390 291 3389 292 3389 293 3391 294 3388 -16947 16947 295 3389 296 3387 297 3387 298 4048 299 4089 -18300 -18300 300 4090 301 4092 302 4095 303 4094 304 4092 20463 -20463 305 4094 306 4092 307 4093 308 3761 309 3391 19431 19431 310 3387 311 3390 312 3390 313 3390 314 3388 -16945 16945 315 3388 316 3387 317 3384 318 3390 319 4088 -17637 -17637 320 4093 321 4095 322 4094 323 4095 324 4095 20472 -20472 325 4095 326 4095 327 4095 328 4095 329 3390 19770 19770 330 3391 331 3386 332 3387 333 3387 334 3390 -16941 16941 335 3389 336 3387 337 3392 338 3389 339 4086 -17643 -17643 340 4091 341 4095 342 4094 343 4095 344 4093 20468 -20468 345 4093 346 4092 347 4090 348 4095 349 3391 19761 19761 350 3388 351 3390 352 3395 353 3391 354 3387 -16951 16951 355 3386 356 3388 357 3388 358 3388 359 4072 -17622 -17622 360 4092 361 4091 362 4092 363 4095 364 4092 20462 -20462 365 4091 366 4095 367 4095 368 4092 369 3408 19781 19781 370 3389 371 3389 372 3389 373 3389 374 3389 -16945 16945 Port closed |
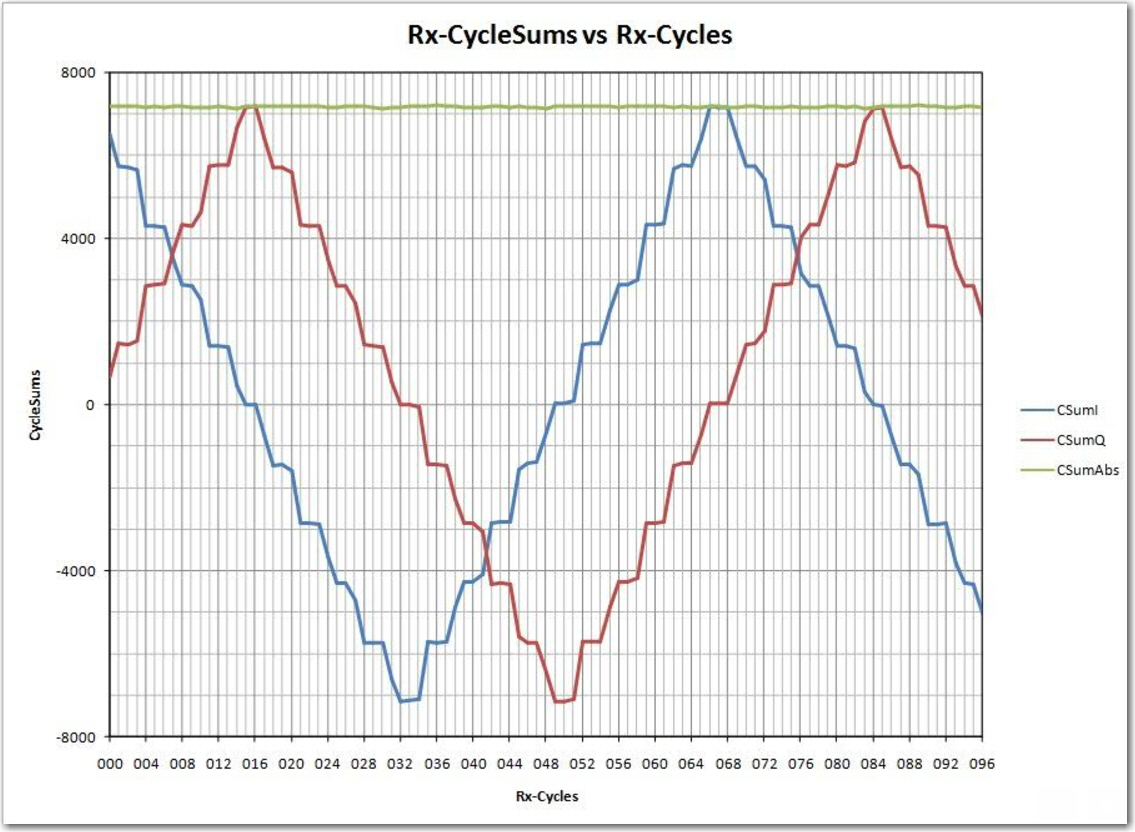
Cycle Sum Accumulation:
As each sample group is summed and the I/Q components generated, accumulate the 1/4-cycle I/Q sums into a ‘Cycle Sum’. As the following printout shows, this step also is being performed properly
Running Sum Accumulation:
The last step in the algorithm is to compute the N-cycle running sum of all the cycle sums. This is done by subtracting the oldest value from the circular buffer from the current running sum, adding the current cycle sum to the running sum, and then replacing the oldest cycle sum value in the circular buffer by the current cycle sum.
- RunningSum = RunningSum + CurrentCycleSum – OldestCycleSum
- OldestCycleSum = CurrentCycleSum
- Circular buffer index incremented by 1 (MOD N)
This one took a while to instrument properly. I first tried just adding some more columns on to the current display setup, but that became too cumbersome, too fast. Verifying the running sum calculation requires looking at not only the current running sum, but also its value from N cycles (or N*5*4 samples) previously. So, I modified the code to only print one line per cycle, and this was much easier to manage. Here’s a partial printout showing a little over 200 cycles, representing about 400mSec (200 cycles * 2mSec/cycle).
To analyze these results, I dropped them into Excel, and used it’s ‘Freeze Panes’ feature to juxtapose the results from cycles 0 through 4 with cycles 65, 66, and 67. This allowed me to verify that the running sum expression was being calculated correctly and the circular buffer was being loaded and referenced correctly. When I finished verifying these results, I plotted the final value column, as shown below:
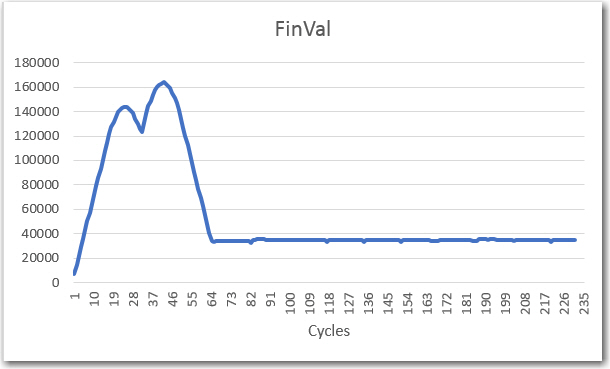
New ‘Final Value’ results
As an experiment, I also momentarily blocked the IR path with my finger, and plotted the results, as shown below:

Filter response with finger blocking IR path for a few seconds, then removed
And again, just waving my finger into and out of the IR path several times over several seconds
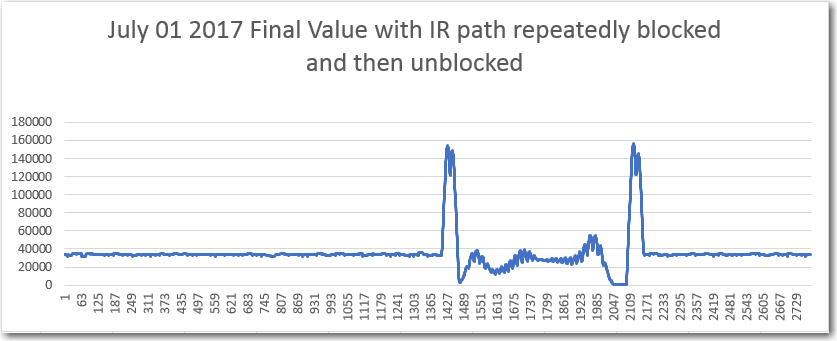
Filter response with finger moved in and out of IR path several times over 3-5 seconds
John’s comment on all this was “still not right”, as explained below:
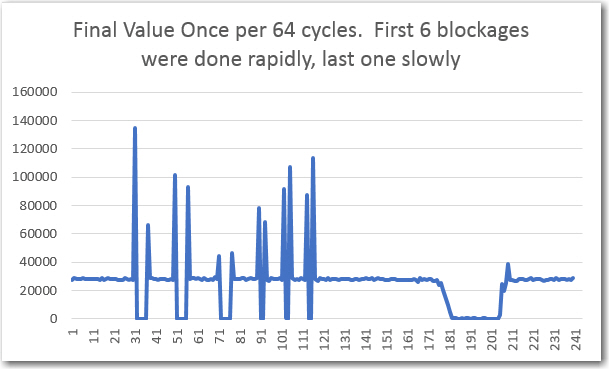
My take on the above was that it is the print statements that are the cause of the problem, not anything to do with Teensy ADC speed. To test this theory, I removed all but the ‘Final Value’ print statement, and put that one statement in a block that executed only once per 64 cycles. With this change, I could see that the print output was keeping up with real time and not lagging as before. Below shows a plot with several IR beam block/unblock cycles, and it appears that the ‘Final Value’ output is much more responsive to the block/unblock events. Interestingly, it appears there is some sort of Gibbs phenomenon associated with the ‘fast’ cycles when the system switches between one equilibrium level and another.
Output from Teensy 3.5 DAC0 (A21) pin
So, now I know that the DAC output works – now I just need to scale the ‘Final Value’ numbers correctly and connect them to the DAC output. Then I can watch the filter action in real time without worrying about the impact of print statements.
With an input square wave amplitude of about 0.35V p-p, or about 0.35/3.3 = 0.106 FS, the output is about 29,000. Therefore the peak output from the FV stage should be about 29,000/0.106 ~ 273,584. so an input of 0.35/3.3 = 0.106 should produce an output of (29,000/273584) *3.3 = 0.106*3.3 = 0.35
So, I modified my Sinewave test code to output the Final Value number, scaled by 273,584, and got the following display. In this test, the input amplitude is about 0.35V p-p, and the output is about 0.35VDC
Stay tuned,
Frank
